
( Jälkikäteen lisätty huomautus : Tämän jutun aloittaminen johtui alunperin väärinkäsityksestä, ei ole todellista ongelmaa! )
Tuntuu että olen kohdannut sellaisen potentiaalisen ongelman että Elementtimenetelmän perusteiden kurssilla käytetty tasoristikon ratkaisumenetelmä ei ehkä sellaisenaan toimisi jos rakenteessa onkin 5 globaalia vapausastetta. On mahdollista että tenttitehtävässä on juurikin ne 5 (todellista) globaalia vapausastetta, joten koetan tässä varmistaa että on olemassa toimiva ratkaisu sellaiseen tapaukseen.
Kurssilla on tasoristikolle käytetty lähteestä kopioitua rotaatiomatriisia [B] jonka dimensio on 4x4. Tämän matriisin [B] avulla on mm. laskettu globaaleista solmusiirtymistä elementtien lokaalit solmusiirtymät. Ja sehän toimii ihan hienosti kun järjestelmän globaaleja vapausasteita on esimerkiksi 2, 3 tai 4. Täytyy vaan sijoittaa arvot oikeisiin vapausasteisiin.
Mielestäni ei ole yksityiskohtaisesti käyty läpi kinemaattisen matriisin [B] muodostamista. Niinpä joku voi törmätä tentissä ongelmaan jos yrittää ratkaista viiden vapausasteen solmusiirtymiä suoraan 4x4 kinemaattisen matriisin [B] avulla. Sellainen ei voi suoraan onnistua. Olisiko mahdollista laatia 5x5 suuruinen matriisi joka tuottaisi lokaalit solmusiirtymät suoraan rakenteen globaaleista siirtymistä?
Mistä siis kenkä puristaa? Aloitetaan ongelman setviminen siitä kohdasta kun on jo laskettu globaalit solmusiirtymät globaalin jäykkyysmatriisin käänteismatriisin [K]-1 ja kuormitusvektorin {F} kertolaskulla eli {U} = [K]-1 {F}
Tuloksena on siis koko järjestelmän globaali solmusiirtymävektori {U} jossa viiden globaalin vapausasteen tapauksessa olisi 5 alkiota.
Miten kerrot 4x4 matriisilla 5-alkioisen pystyvektorin? (et mitenkään) Miten sijoitat 5 vapausastetta vain nelialkioiseen pystyvektoriin?
Sitten muodostetaan jokaiselle elementille oma solmusiirtymävektori {u} globaaleista tiedoista mutta lokaaleihin vapausasteisiin ...
Öööh ... olenkohan munaamassa itseni oikein perusteellisesti ...
Tässä vaiheessa alkaa tuntua että olen muistiossani sittenkin joron jäljillä. Ongelmaa ei olekaan olemassa?
Justihin joo, ainoastaan ne alkiot valitaan koko järjestelmän globaalista pystyvektorista {U} kunkin elementin omaan (mutta globaaleja tietoja sisältävään) pystyvektoriin {u} jotka ovat ko. elementin lokaalien vapausasteiden mukaisia.
Hämmentävää. Globaalit ja lokaalit ja varsinkin nämä lokaaleissa vapausasteissa olevat globaalit tiedot koituvat vielä kohtalokseni.
Tarkemmin ajatellen ei siinä sittenkään taida olla mitään erikoisempaa ongelmaa. En vaan selkeästi tajunnut sitä että {U} ja {u} ovat eri vektoreita. Molemmissa on globaaleja tietoja, mutta {U} on rakenteen globaalien vapausasteiden mukainen ja {u} on kunkin elementin omien lokaalien vapausasteiden mukainen.
Globaalien solmusiirtymien vektorissa {U} on niin monta alkiota kuin mitä on globaaleja vapausasteita. Elementin omien solmusiirtymien vektorissa {u} on vain ne alkiot jotka sisältyvät elementin neljään vapausasteeseen. Niinpä 4x4 kinemaattinen matriisi [B] riittää aivan mainiosti. Vaara ohi.
Ehkä minun pitäisi kurssin opettajan K.Kiven tavoin ilmoittaa että sitten kun olen pissannut julkisesti housuihini, tulen hakemaan teiltä puoltoa eläkehakemukseeni?
Noh, tämä voi kuitenkin lopulta olla opettavainen tarina, joten aion säilyttää tämän kirjoitelman kaikesta huolimatta. Näin sekaisin ihmisparka voi mennä kun aikansa pohtii globaaleja ja lokaaleja rinnakkain.
Mitä teen pelastaakseni kasvoni tämän murskaavan kämmin jälkeen? Yritän kääntää tappioni voitoksi, kohota itsekunnioitukseni tuhkasta uusin voimin kuni Fenix-lintunen!
Kerrataanpa tunneilla tasoristikolle käytettyä ratkaisumenetelmää oleellisilta osin. Ohitetaan alku ja todetaan että järjestelmän globaalit solmusiirtymät ovat pystyvektorina {U} = [K]-1 {F} ja tästä on siirryttävä tarkastelemaan rakenteen sauvoja lokaalisti.

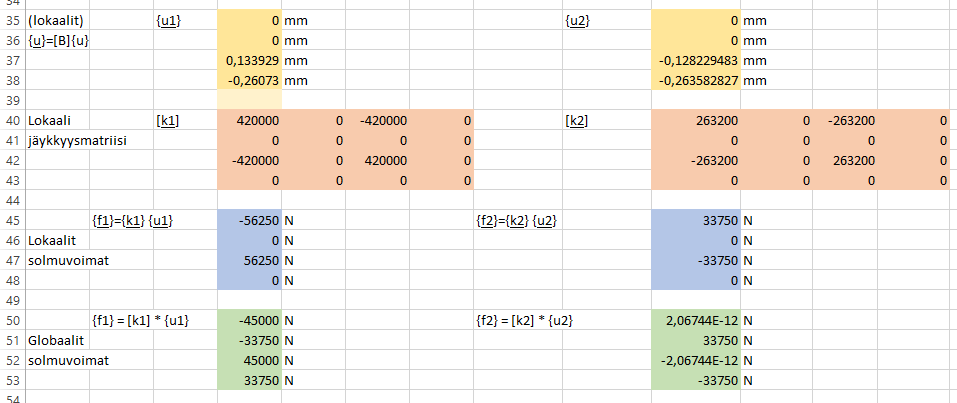
Yllä on näyte Excel-taulukosta jossa on laskettu harjoitustehtävää FES09H1. Se on yksinkertainen 2-elementtinen tasoristikko jossa oikeasti on vain kaksi globaalia vapausastetta, joten globaali jäykkyysmatriisi on pelkistettävissä kokoon 2x2. Ainoastaan sauvojen loppusolmuissa olevat lokaalit vapausasteet 3 ja 4 toteutuvat koska alkusolmut ovat kiinnitettyjä. Niinpä globaalit solmusiirtymät sijoitetaan ratkaisun jälkeen järjestelmän pystyvektorista {U} elementtien loppusolmujen pystyvektoreihin {u} lokaaleihin vapausasteisiin 3 ja 4 eli kolmanteen ja neljänteen riviin. Sauvojen alkusolmujen lokaaleihin vapausasteisiin 1 ja 2 jää pelkät nollat.
Erehdyksestä viisastuneena painotamme erikoisen ankarasti sitä että sauvaelementissä on lokaalisti aina 4 vapausastetta riippumatta siitä miten monta globaalia vapausastetta rakennelmassa on. Sauvaelementin pystyvektorissa on vapausasteiden mukaiset 4 riviä. Kinemaattinen matriisi [B] kuuluu sauvaelementille olla 4x4 matriisi jossa on rivejä ja sarakkeita kumpiakin sama määrä, juurikin se sauvan lokaalien vapausasteiden mukainen neljä.
Jos rakennelmalla olisi kokonaista viisi globaalia vapausastetta niin elementtien jäykkyysmatriisit [k] olisivat 4x4 kuten sauvalle ja sen neljälle vapausasteelle kuuluu ja niistä muodostettaisiin sijoittelusummauksella järjestelmän globaali jäykkyysmatriisi [K] jonka dimensio olisi 5x5 globaalien vapausasteiden määrän mukaan. Kuormituksen pystyvektori {F} olisi myös jaettava viiden globaalin vapausasteen mukaisesti komponentteihin, joten se olisi 5-rivinen pystyvektori. Kertolaskusta {U} = [K]-1 {F} syntyvä globaali solmusiirtymävektori olisi myös 5-rivinen pystyvektori globaaleiden vapausasteiden määrän mukaan.
Ja sitten olisi ryhdyttävä miettimään elementtikohtaisesti että miten muodostetaan 4-riviset elementtien pystyvektorit {u}. Niihin tarvitsee vaan kopioida arvoja järjestelmän solmusiirtymät sisältävästä {U} -vektorista, mutta elementtien toteutuvat vapausasteet huomioiden. Jos elementin tietty solmu ei oikeasti pääse liikkumaan kiinnityksen vuoksi, niin siihen ei globaalisti voi tulla solmusiirtymää.
Periaatteessa tämä on mielestäni tavallaan käänteinen prosessi sille miten sauvojen jäykkyysmatriiseista [k] muodostettiin rakenteen globaali jäykkyysmatriisi [K]. Globaalit vapausasteet mapataan kunkin sauvaelementin lokaaleihin vapausasteisiin samalla periaatteella mutta eri suuntaan. Jos globaaleja vapausasteita on 5 ja sauvoissa on 4 vapausastetta niin eihän kaikki globaalit vapausasteet voi mitenkään toteutua missään sauvassa, mutta eipä tarvitsekaan.
Ihan zuluna vedän tällaisen esimerkin. Jos tietyn sauvan lokaalit vapausasteet mapataan kokonaisuuden globaaleihin viiteen vapausasteeseen vaikkapa näin (nolla tarkoittaa ettei tieto oikeasti mene minnekään):
| lokaali | -> | globaali |
|---|---|---|
| 1 | -> | 0 |
| 2 | -> | 0 |
| 3 | -> | 1 |
| 4 | -> | 2 |
... niin päinvastaiseen suuntaan eli globaaleista lokaaleihin siirryttäessä globaalit vapausasteet 1 ja 2 menisivät sen sauvan lokaaleihin vapausasteisiin 3 ja 4. Jos sauvan lokaalit vapausasteet eivät alunperinkään menneet vapausasteisiin 3, 4 ja 5 niin eipä noista globaaleista vapausasteista voi takaisin sen sauvan lokaaleihin vapausasteisiin jatkossakaan tulla mitään.

Millainen sauva-elementti on lokaalisti? Keskittykäämme hetkeksi siihen. Sauvaelementillä on lokaalisti neljä vapausastetta joten se voidaan esittää 4-alkioisena pystyvektorina. Alkusolmun vapausasteet 1 ja 2 ovat pystyvektorin ekalla ja tokalla rivillä ja loppusolmun vapausasteet 3 ja 4 ovat pystyvektorin kolmannella ja neljännellä rivillä. Vapausasteet 1 ja 3 ovat lokaalisti X-suuntaisia ja vapausasteet 2 ja 4 ovat Y-suuntaisia sauvan omassa lokaalissa koordinaatistossa.
Ristikkorakenteessa käytetty sauva on sikäli erikoinen että se ei tarjoa solmuissaan lainkaan tukimomenttia. Sauvassa on ainoastaan normaalijännitys, joko aksiaalista vetoa tai aksiaalista puristusta. Solmut, joissa rakenteen sauvat liittyvät toisiinsa, ajatellaan kitkattomiksi niveliksi jotka eivät välitä momenttia. Periaatteessa sauva pääsee vapaasti kääntymään solmun ympäri (ainakin pienehkön kulman) koska solmu on tukimomenttia tarjoamaton nivel.
Varsinaisesti elementtimenetelmä tässä yhteydessä haluaa käsitellä ainoastaan lineaarisia muutoksia joten muutokset rakenteessa pidetään melko pieninä. Ei ole tarkoitus tutkia miten ristikko hajoaa.
Tavoite on ennenkaikkea elementtien lokaalit tiedot koska haluamme selvittää elementtikohtaisen normaalijännityksen ja tukireaktiot.
Olemme siis laskeneet elementeille lokaalit solmusiirtymät kertomalla kinemaattisella matriisilla [B] joka tasoristikolle on 4x4 matriisi. Saamme lokaalit solmusiirtymät kaavalla {u} = [B] {u}
Huomattakoon että Excel-taulukoissa eräät arvot ovat käytännössä nollia, esim. 2,06E-12 on itseisarvoltaan erittäin pieni luku koska se on suuruusluokkaa 10-12, säpinää vasta kahdennessatoista desimaalissa. Laskutarkkuuden puitteissa se on pelkkä nolla.
Ylä- ja alaindeksejä ei näissä Excel-näytteissä ole käytetty vaikka se lie Excelissäkin mahdollista. Esimerkiksi [k1] tarkoittaa oikeasti [k]1 ja käänteismatriisi [K]-1 on merkitty [K]^-1
Huomaa alleviivaukset lokaalien tunnusten kohdalla, kuten {f}, {u}, [k] ja alleviivauksen puuttuminen vastaavien globaalien tunnusten kohdalla kuten {f}, {u}, [k].
Haluaisimme päästä elementtien lokaaleihin solmuvoimiin {f} joille sinänsä pätee kaava {f} = [B] {f}, mutta emme voi sitä käyttää koska emme tätä laskentatapaa noudattaessamme toistaiseksi tunne elementtien globaaleja solmuvoimia {f}.
Niinpä sovellamme kaavaa {f} = [k] {u} jossa [k] on elementin lokaali jäykkyysmatriisi. Alussahan on ratkaistu elementtien jäykkyysmatriisit [k], mutta näissä on globaalit koordinaatit, joten emme voi käyttää niitä tässä yhteydessä. Elementin lokaalin jäykkyysmatriisin [k] muodostaa helpostikin kunhan tuntee ko. elementin jäykkyysvakion k = E·A / L
| [k] | = |
| Ainoastaan ensimmäisellä ja kolmannella rivillä ja sarakkeella olevat nollasta poikkeavat arvot kuvastavat sitä että lokaalisti sauva-elementissä on jäykkyyttä ainoastaan ensimmäisessä ja kolmannessa vapausasteessa eli alku- ja loppusolmujen X-suuntaisissa vapausasteissa. Y-suunnassa jäykkyyttä ei sauvassa lokaalisti ole, sitä todistavat pelkät nollat toisella ja neljännellä rivillä ja sarakkeella, eli alku- ja loppusolmujen toisessa ja neljännessä vapausasteessa. |
Kun olemme ratkaisseet elementtien lokaalit solmuvoimat lokaalien tietojen avulla kaavalla {f} = [k] {u}, saamme elementtien globaalit solmuvoimat helposti kaavalla {f} = [k] {u} jossa siis käytämme nimenomaan elementtien (globaaleja) matriiseja [k] ja elementtien globaaleja solmusiirtymiä {u}.
Sauvassa voi lokaalisti olla solmuvoima vain vapausasteissa 1 ja 3 eli lokaalissa X-suunnassa. Kun sauvassa ei ole elementtikuormaa niin lokaalisti X-suunnan voimien tulee kumota toisensa eli ne ovat toistensa vastalukuja. Kukin elementti täytyy nimittäin olla tasapainossa.
Jos alkusolmuun lokaalisti vaikuttava X-suunnan voima on negatiivinen (vaikuttaa vasemmalle) ja loppusolmuun vaikuttava voima positiivinen (vaikuttaa oikealle) niin sauvassa on vetorasitus. Jos taas alkusolmuun lokaalisti (vapausaste 1) vaikuttaa positiivinen voima ja loppusolmuun (vapausaste 3) negatiivinen voima, niin sauvassa on puristusta.
Lopuksi haluan tarkastella kurssin opetusta ja käytettyä ratkaisumenetelmää kriittisesti, mutta tokikin rakentavassa hengessä.
Oppimisjärjestelmä Moodlessa PDF-tiedostoina oleva (osin, ei koko) oppikirja noudattaa jonkin verran eri menetelmää kuin mitä kurssin lähiopetuksessa toteutettiin. Kirjassa käytetään yhtälöryhmien ratkaisua, eikä käänteismatriisilla kertomista. Kirja on hiukan korkealentoinen ja akateeminen. Sikäli oppikirjasta ei saa mahdollisimman suurta tukea. Sieltä kuitenkin näkee miten muodostetaan esim. rotaatiomatriisi [B] eli ns. kinemaattinen matriisi. Ja tarjoaahan se vaihtoehtoisen näkökulman aiheeseen.
Kurssilla on laskelmien tekemisessä tukeuduttu Excel-taulukkolaskentaan. Se tekee esim. matriisin kääntämisestä sekä matriisin ja pystyvektorin kertolaskusta helppoa. Ratkaisumenetelmän dokumentointi kuitenkin mielestäni hiukan onnahtaa jos se on pelkästään Excel-tiedoston varassa. Pitäisin omien muistiinpanojen ylläpitoa tärkeänä tuolla melko tiivistahtisella kurssilla. Excel-taulukko ei oikein kelpaa opiskelun dokumentoinniksi koska se on kuitenkin hiukan takkuinen luettava eikä se tarjoa vastausta kysymykseen "miksi?".
Excelissä tärkeitä funktioita ovat (kieliversiosta riippuen) mm. MINVERSE eli MKÄÄNTEINEN, MMULT eli MKERRO matriisien ja vektoreiden käsittelyssä. Matriisien kanssa oleellinen alueiden valinta ja näppäily-yhdistelmä Ctrl + Shift + Enter on tullut hyvin opeteltua. Excelissä on syytä pitää mielessä että se käsittelee kulmia radiaaneina. Astemuunnokset täytyy tehdä tarvittaessa erikseen. Solun kaava alkaa yhtäsuuruus-merkillä ja desimaalierottimena on meikäläisissä oloissa syytä käyttää pilkkua.
Omat muistiinpanot ovat tärkeitä, mutta vielä paremmin asiat oppinee jos tekee omia ohjelmia tehtävien ratkaisuun esim. JavaScript-kielellä (kuten näillä sivuilla hiukan olen koettanut tehdä). Tosin silloin joutuu takkuamaan monien muidenkin asioiden kansssa kuin varsinaisen elementtimenetelmän bisneslogiikan kanssa. Ohjelman rakentamisessa on moninkertainen työ Excel-taulukkoon nähden ja ohjelmastakin on vaikea tehdä yleispätevää. Ratkaisun joutuu rakentamaan tietylle tapaukselle ja toisenlainen tapaus vaatii erilaiset ratkaisut. Omat ongelmansa ohjelmoimalla ratkaisemisessakin siis on, mutta paatuneelle ohjelmoijalle se on luonnollinen valinta.
Erikoisesti JavaScriptin suhteen huomiota vaatii mm. käänteismatriisin toteuttaminen ja se että matriisien ja vektoreiden välillä on tehtävä ero. Excel käsittelee matriiseja ja vektoreita oleellisesti samalla tavalla mutta JavaScriptissä ei esimerkiksi voi luoda sellaista taulukkoa joka olisi kaksiulotteinen mutta riveillä olisi vain yksi alkio. Voi toki yrittää seuraavaa:
// var a, b, c; var V = new Array ( new Array ( a ), new Array ( b ), new Array ( c ) );
... eikä se ole syntaktisesti väärin, mutta lopputulos ei kuitenkaan ehkä ole ihan sitä mitä toivottiin.
En ole kokeillut missä määrin ohjelmoitavaa graafista laskinta voisi käyttää apuna pienehköjen tehtävien ratkaisussa, mutta ajatuksena mielenkiintoinen.
Kuvioiden piirtely on oma alueensa. Kuviot on kurssilla tietääkseni täytynyt piirtää käsin paperille. Kotitehtävissä paperipiirros on ohjeen mukaan napattu kännykkäkameralla ja liitetty Excel-taulukon kanssa samaan pakattuun ZIP-tiedostoon sekä palautettu oppimisjärjestelmä Moodleen.
Suttupaperia pitäisin tarpeellisena apuvälineenä tehtävien ratkaisussa. Tavalliselle funktiolaskimellekin voi olla käyttöä.
En vielä tiedä miten hyvin oppi on kurssilla mennyt perille, joten en voi langettaa lopullista tuomiota tästä menetelmästä. Tentti on aivan näillä näppylöillä, mutta taitojen varsinaisen koetinkiven palauttamiseen on siitä vielä kokonainen kuukausi aikaa. Harmittamaan vaan jää se että avaruusristikot ja avaruuskehät jäävät kurssilla kokonaan käsittelemättä. Vaativuudeltaan huippua kurssilla on yksinkertaisen 3-palkkisen tasokehän ratkaisu elementtikuormituksin.
Pelkästään käänteismatriisin käyttöön en ole täysin tyytyväinen. Se on Excelillä helppoa, ainakin pienten matriisien tapauksessa, mutta jos alkioita olisi todella paljon niin minusta matriisin kääntäminen olisi suhteellisen vaatimattomin resurssein esim. JavaScript-ohjelmassa huono vaihtoehto. Ohjelmoijalle mielestäni olisi tärkeää opetella ratkaisu yhtälöryhmien kautta koska se oletettavasti on isoilla matriiseilla huomattavasti taloudellisempaa.
Hyvänä pidän kurssia sikäli että siinä todella sai konkreettisen tuntuman elementtimenetelmän periaatteisiin. Aksiaalisesta sauvasta aloittaminen on minusta ihan hyvä ratkaisu, vaikka sillä ei sinänsä mitään käyttöä olekaan. Ainakin pienemmille järjestelmille globaaleihin vapausasteisiin keskittyminen ja käytännöllinen ratkaisu on hyvä ja oikeaa oivallusta nopeasti tarjoava vaihtoehto. Kireä aikataulu on epäilemättä rasite.
Monimutkaisemmille rakenteille (esim. 3-ulotteiset kuorirakenteet) tällainen laskennan etenemisen osalta suhteellisen havainnollinen Excel-tyyppinen ratkaisu käy nopeasti käytännössä mahdottomaksi kun järjestelmä muuttuu vaativammaksi. Silloin tarvitaan järeämpiä työkaluja, mutta toimintojensa teknisen toteuttamisen osalta ne ovat epähavainnollisempia, käyttäjä ei nää mitä julkisivun takana varsinaisesti tapahtuu. Niitäkin tsydeeemejä on mahdollista käyttää väärin, jopa aivan päin helvettiä, joten järki ja osaaminen täytyy niissäkin olla mukana. Korskea tulostus ei todista että olisi laskettu oikein.